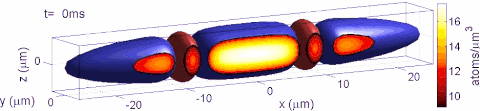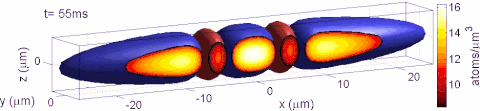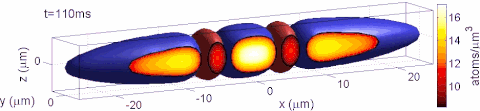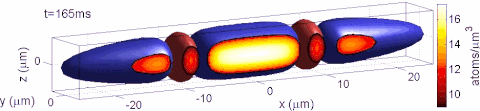
{\displaystyle {\frac {\Delta V}{V_{0}}}={\frac {\left(1+\varepsilon _{11}+\varepsilon _{22}+\varepsilon _{33}+\varepsilon _{11}\cdot \varepsilon _{22}+\varepsilon _{11}\cdot \varepsilon _{33}+\varepsilon _{22}\cdot \varepsilon _{33}+\varepsilon _{11}\cdot \varepsilon _{22}\cdot \varepsilon _{33}\right)\cdot a^{3}-a^{3}}{a^{3}}}}

For prescribed strain components ε i j \varepsilon _{ij} the strain tensor equation u i , j + u j , i = 2 ε i j {\displaystyle u_{i,j}+u_{j,i}=2\varepsilon _{ij}} represents a system of six differential equations for the determination of three displacements components u i

u_{i}, giving an over-determined system. Thus, a solution does not generally exist for an arbitrary choice of strain components. Therefore, some restrictions, named compatibility equations, are imposed upon the strain components. With the addition of the three compatibility equations the number of independent equations are reduced to three, matching the number of unknown displacement components. These constraints on the strain tensor were discovered by Saint-Venant, and are called the "Saint Venant compatibility equations".

The compatibility functions serve to assure a single-valued continuous displacement function u i u_{i}. If the elastic medium is visualised as a set of infinitesimal cubes in the unstrained state, after the medium is strained, an arbitrary strain tensor may not yield a situation in which the distorted cubes still fit together without overlapping.